OpenVMS VAX RTL Mathematics (MTH$) Manual

Document revision date: 19 July 1999

OpenVMS VAX RTL Mathematics (MTH$) Manual

Contents

Index

BLAS1$VxROTG

The Generate the Elements for a Givens Plane Rotation routine constructs a Givens plane rotation that eliminates the second element of a two-element vector.

Format

BLAS1$VSROTG a ,b ,c ,s

BLAS1$VDROTG a ,b ,c ,s

BLAS1$VGROTG a ,b ,c ,s

BLAS1$VCROTG a ,b ,c ,s

BLAS1$VZROTG a ,b ,c ,s

BLAS1$VWROTG a ,b ,c ,s
Use BLAS1$VSROTG for single-precision real operations.
Use BLAS1$VDROTG for double-precision real (D-floating) operations.
Use BLAS1$VGROTG for double-precision real (G-floating) operations. Use BLAS1$VCROTG for single-precision complex operations.
Use BLAS1$VZROTG for double-precision complex (D-floating) operations.
Use BLAS1$VWROTG for double-precision complex (G-floating) operations.

RETURNS

None.

Arguments

a

OpenVMS usage: floating_point or complex_number

type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex

access: modify

mechanism: by reference

On entry, first element of the input vector. On exit, rotated element r . The a argument is the address of a floating-point or floating-point complex number that is this vector element.
Specify the data type as follows:

Routine Data Type for a

BLAS1$VSROTG F-floating real

BLAS1$VDROTG D-floating real

BLAS1$VGROTG G-floating real

BLAS1$VCROTG F-floating complex

BLAS1$VZROTG D-floating complex

BLAS1$VWROTG G-floating complex

b

OpenVMS usage: floating_point or complex_number

type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex

access: modify

mechanism: by reference

On entry, second element of the input vector. On exit from BLAS1$VSROTG, BLAS1$VDROTG, and BLAS1$VGROTG, reconstruction element z . (See the Description section for more information about z .) The b argument is the address of a floating-point or floating-point complex number that is this vector element.
Specify the data type as follows:

Routine Data Type for b

BLAS1$VSROTG F-floating real

BLAS1$VDROTG D-floating real

BLAS1$VGROTG G-floating real

BLAS1$VCROTG F-floating complex

BLAS1$VZROTG D-floating complex

BLAS1$VWROTG G-floating complex

c

OpenVMS usage: floating_point

type: F_floating, D_floating, or G_floating real

access: write only

mechanism: by reference

First rotation element, which can be interpreted as the cosine of the angle of rotation. The c argument is the address of a floating-point or floating-point complex number that is this vector element.
Specify the data type (which is always real) as follows:

Routine Data Type for c

BLAS1$VSROTG and BLAS1$VCROTG F-floating real

BLAS1$VDROTG and BLAS1$VZROTG D-floating real

BLAS1$VGROTG and BLAS1$VWROTG G-floating real

s

OpenVMS usage: floating_point or complex_number

type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex

access: write only

mechanism: by reference

Second rotation element, which can be interpreted as the sine of the angle of rotation. The s argument is the address of a floating-point or floating-point complex number that is this vector element.
Specify the data type as follows:

Routine Data Type for s

BLAS1$VSROTG F-floating real

BLAS1$VDROTG D-floating real

BLAS1$VGROTG G-floating real

BLAS1$VCROTG F-floating complex

BLAS1$VZROTG D-floating complex

BLAS1$VWROTG G-floating complex

Routine	Data Type for a
BLAS1$VSROTG	F-floating real
BLAS1$VDROTG	D-floating real
BLAS1$VGROTG	G-floating real
BLAS1$VCROTG	F-floating complex
BLAS1$VZROTG	D-floating complex
BLAS1$VWROTG	G-floating complex

Routine	Data Type for b
BLAS1$VSROTG	F-floating real
BLAS1$VDROTG	D-floating real
BLAS1$VGROTG	G-floating real
BLAS1$VCROTG	F-floating complex
BLAS1$VZROTG	D-floating complex
BLAS1$VWROTG	G-floating complex

Routine	Data Type for c
BLAS1$VSROTG and BLAS1$VCROTG	F-floating real
BLAS1$VDROTG and BLAS1$VZROTG	D-floating real
BLAS1$VGROTG and BLAS1$VWROTG	G-floating real

Routine	Data Type for s
BLAS1$VSROTG	F-floating real
BLAS1$VDROTG	D-floating real
BLAS1$VGROTG	G-floating real
BLAS1$VCROTG	F-floating complex
BLAS1$VZROTG	D-floating complex
BLAS1$VWROTG	G-floating complex

Description

BLAS1$VSROTG, BLAS1$VDROTG, and BLAS1$VGROTG construct a real Givens plane rotation. BLAS1$VCROTG, BLAS1$VZROTG, and BLAS1$VWROTG construct a complex Givens plane rotation. The Givens plane rotation eliminates the second element of a two-element vector. The elements of the vector are real or complex single-precision or double-precision (D and G) numbers. The routine name determines the data type you should specify for arguments a, b, and s. Specify the same data type for each of these arguments.
BLAS1$VSROTG, BLAS1$VDROTG, and BLAS1$VGROTG can use the reconstruction element z to store the rotation elements for future use. There is no counterpart to the term z for BLAS1$VCROTG, BLAS1$VZROTG, and BLAS1$VWROTG.
The BLAS1$VxROTG routines can be used to introduce zeros selectively into a matrix.
For BLAS1$VDROTG, BLAS1$VGROTG, BLAS1$VZROTG, and BLAS1$VWROTG (the double-precision routines), the elements of the vector are scaled to avoid intermediate overflow or underflow. BLAS1$VSROTG and BLAS1$VCROTG (the single-precision routines) use a backup data type to avoid intermediate underflow or overflow, which may cause the final result to differ from the original Fortran routine.
BLAS1$VSROTG, BLAS1$VDROTG, and BLAS1$VGROTG --- Real Givens Plane Rotation

Given the elements a and b of an input vector, BLAS1$VSROTG, and BLAS1$VDROTG, BLAS1$VGROTG calculate the elements c and s of an orthogonal matrix such that:

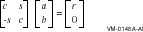
A real Givens plane rotation is constructed for values a and b by computing values for r , c , s , and z , as follows:

________ r = p / 2 2 \/ a + b

where:

p =SIGN(a) if |a| > |b|

p =SIGN(b) if |a|<=|b|

c = a r
if r <> 0

c = 1 if r = 0

s = b r
if r <>0

s = 0 if r = 0

z = s if |a| > |b|

z = 1 c
if |a|<=|b| and c <>0 and r <>0

z = 1 if |a|<=|b| and c = 0 and r <>0

z = 0 if r = 0

BLAS1$VSROTG, BLAS1$VDROTG, and BLAS1$VGROTG can use the reconstruction element z to store the rotation elements for future use. The quantities c and s are reconstructed from z as follows:

For |z| = 1, c = 0 and s = 1.0

_______ For |z| < 1, c= / 2 and s = z \/ 1 - z

1 ________ For |z| > 1, c = - and s = / 2 z \/ 1 - c

The arguments c and s can be passed to the BLAS1$VxROT routines.

BLAS1$VCROTG, BLAS1$VZROTG, and BLAS1$VWROTG --- Complex Givens Plane Rotation

Given the elements a and b of an input vector, BLAS1$VCROTG, BLAS1$VZROTG, and BLAS1$VWROTG calculate the elements c and s of an orthogonal matrix such that:

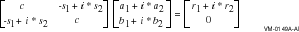
There are no BLAS Level 1 routines with which you can use complex c and s arguments.

Example


C C To generate the rotation elements for a vector of C elements a and b: C REAL A,B,C,S CALL SROTG(A,B,C,S)

BLAS1$VxSCAL

The Scale the Elements of a Vector routine computes a*x where a is a scalar number and x is an n-element vector.

Format

BLAS1$VSSCAL n ,a ,x ,incx

BLAS1$VDSCAL n ,a ,x ,incx

BLAS1$VGSCAL n ,a ,x ,incx

BLAS1$VCSCAL n ,a ,x ,incx

BLAS1$VCSSCAL n ,a ,x ,incx

BLAS1$VZSCAL n ,a ,x ,incx

BLAS1$VWSCAL n ,a ,x ,incx

BLAS1$VZDSCAL n ,a ,x ,incx

BLAS1$VWGSCAL n ,a ,x ,incx
Use BLAS1$VSSCAL to scale a real single-precision vector by a real single-precision scalar. Use BLAS1$VDSCAL to scale a real double-precision (D-floating) vector by a real double-precision (D-floating) scalar.
Use BLAS1$VGSCAL to scale a real double-precision (G-floating) vector by a real double-precision (G-floating) scalar. Use BLAS1$VCSCAL to scale a complex single-precision vector by a complex single-precision scalar.
Use BLAS1$VCSSCAL to scale a complex single-precision vector by a real single-precision scalar. Use BLAS1$VZSCAL to scale a complex double-precision (D-floating) vector by a complex double-precision (D-floating) scalar.
Use BLAS1$VWSCAL to scale a complex double-precision (G-floating) vector by a complex double-precision (G-floating) scalar.
Use BLAS1$VZDSCAL to scale a complex double-precision (D-floating) vector by a real double-precision (D-floating) scalar.
Use BLAS1$VWGSCAL to scale a complex double-precision (G-floating) vector by a real double-precision (G-floating) scalar.

RETURNS

None.

Arguments

n

OpenVMS usage: longword_signed

type: longword integer (signed)

access: read only

mechanism: by reference

Number of elements in vector x to be scaled. The n argument is the address of a signed longword integer containing the number of elements to be scaled. If you specify a value for n that is less than or equal to 0, then x is unchanged.
a

OpenVMS usage: floating_point or complex_number

type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex

access: read only

mechanism: by reference

Scalar multiplier for the elements of vector x . The a argument is the address of a floating-point or floating-point complex number that is this multiplier.
Specify the data type as follows:

Routine Data Type for a

BLAS1$VSSCAL and BLAS1$VCSSCAL F-floating real

BLAS1$VDSCAL and BLAS1$VZDSCAL D-floating real

BLAS1$VGSCAL and BLAS1$VWGSCAL G-floating real

BLAS1$VCSCAL F-floating complex

BLAS1$VZSCAL D-floating complex

BLAS1$VWSCAL G-floating complex

If you specify 1.0 for a, then x is unchanged.
x

OpenVMS usage: floating_point or complex_number

type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex

access: modify

mechanism: by reference, array reference

Array containing the elements to be accessed. All elements of array x are accessed only if the increment argument of x, called incx, is 1. The x argument is the address of a floating-point or floating-point complex number that is this array. On entry, this argument is an array of length at least:
1+(n-1)*|incx|
where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine Data Type for x

BLAS1$VSSCAL F-floating real

BLAS1$VDSCAL D-floating real

BLAS1$VGSCAL G-floating real

BLAS1$VCSCAL and BLAS1$VCSSCAL F-floating complex

BLAS1$VZSCAL and BLAS1$VZDSCAL D-floating complex

BLAS1$VWSCAL and BLAS1$VWGSCAL G-floating complex

On exit, x is an array of length at least:
1+(n-1)*|incx|
where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

After the call to BLAS1$VxSCAL, x[i] is replaced by a*x[i] If a shares a memory location with any element of the vector x , results are unpredictable.
incx

OpenVMS usage: longword_signed

type: longword integer (signed)

access: read only

mechanism: by reference

Increment argument for the array x. The incx argument is the address of a signed longword integer containing the increment argument. If incx is greater than 0, then x is referenced forward in array x; that is, x[i] is referenced in:
x(1+(i-1)*incx)
where:

x = array specified in x

i = element of the vector x

incx = increment argument for the array x specified in incx

If you specify a negative value for incx, it is interpreted as the absolute value of incx. If incx equals 0, the results are unpredictable.

Routine	Data Type for a
BLAS1$VSSCAL and BLAS1$VCSSCAL	F-floating real
BLAS1$VDSCAL and BLAS1$VZDSCAL	D-floating real
BLAS1$VGSCAL and BLAS1$VWGSCAL	G-floating real
BLAS1$VCSCAL	F-floating complex
BLAS1$VZSCAL	D-floating complex
BLAS1$VWSCAL	G-floating complex

Routine	Data Type for x
BLAS1$VSSCAL	F-floating real
BLAS1$VDSCAL	D-floating real
BLAS1$VGSCAL	G-floating real
BLAS1$VCSCAL and BLAS1$VCSSCAL	F-floating complex
BLAS1$VZSCAL and BLAS1$VZDSCAL	D-floating complex
BLAS1$VWSCAL and BLAS1$VWGSCAL	G-floating complex

Description

BLAS1$VxSCAL computes a*x where a is a scalar number and x is an n-element vector. The computation is expressed as follows:

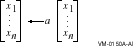
Vector x contains n elements that are accessed from array x by stepping incx elements at a time. The vector x can be a row or a column of a matrix. Both forward and backward indexing are permitted.

The public-domain BLAS Level 1 xSCAL routines require a positive value for incx. The Run-Time Library BLAS Level 1 routines interpret a negative value for incx as the absolute value of incx.

The algorithm does not provide a special case for a = 0. Therefore, specifying 0 for a has the effect of setting to zero all elements of the vector x using vector operations.

Example


C C To scale a vector x by 2.0 using SSCAL: C INTEGER INCX,N REAL X(20),A INCX = 1 A = 2 N = 20 CALL BLAS1$VSSCAL(N,A,X,INCX)

BLAS1$VxSWAP

The Swap the Elements of Two Vectors routine swaps n elements of the vector x with the vector y .

Format

BLAS1$VSSWAP n ,x ,incx ,y ,incy

BLAS1$VDSWAP n ,x ,incx ,y ,incy

BLAS1$VCSWAP n ,x ,incx ,y ,incy

BLAS1$VZSWAP n ,x ,incx ,y ,incy
Use BLAS1$VSSWAP for single-precision real operations.
Use BLAS1$VDSWAP for double-precision real (D or G) operations. Use BLAS1$VCSWAP for single-precision complex operations.
Use BLAS1$VZSWAP for double-precision complex (D or G) operations.

RETURNS

None.

Arguments

n

OpenVMS usage: longword_signed

type: longword integer (signed)

access: read only

mechanism: by reference

Number of elements in vector x to be swapped. The n argument is the address of a signed longword integer containing the number of elements to be swapped.
x

OpenVMS usage: floating_point or complex_number

type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex

access: modify

mechanism: by reference, array reference

Array containing the elements to be accessed. All elements of array x are accessed only if the increment argument of x, called incx, is 1. The x argument is the address of a floating-point or floating-point complex number that is this array. On entry, this argument is an array of length at least:
1+(n-1)*|incx|
where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine Data Type for x

BLAS1$VSSWAP F-floating real

BLAS1$VDSWAP D-floating or G-floating real

BLAS1$VCSWAP F-floating complex

BLAS1$VZSWAP D-floating or G-floating complex

If n is less than or equal to 0, then x and y are unchanged. If any element of x shares a memory location with an element of y , the results are unpredictable.
On exit, x is an array of length at least:
1+(n-1)*|incx|
where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

After the call to BLAS1$VxSWAP, n elements of the array specified by x are interchanged with n elements of the array specified by y.
incx

OpenVMS usage: longword_signed

type: longword integer (signed)

access: read only

mechanism: by reference

Increment argument for the array x. The incx argument is the address of a signed longword integer containing the increment argument. If incx is greater than or equal to 0, then x is referenced forward in array x; that is, x[i] is referenced in:
x(1+(i-1)*incx)
where:

x = array specified in x

i = element of the vector x

incx = increment argument for the array x specified in incx

If incx is less than 0, then x is referenced backward in array x; that is, x[i] is referenced in:
x(1+(n-i)*|incx|)
where:

x = array specified in x

n = number of vector elements specified in n

i = element of the vector x

incx = increment argument for the array x specified in incx

y

OpenVMS usage: floating_point or complex_number

type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex

access: modify

mechanism: by reference, array reference

Array containing the elements to be accessed. All elements of array y are accessed only if the increment argument of y, called incy, is 1. The y argument is the address of a floating-point or floating-point complex number that is this array. On entry, this argument is an array of length at least:
1+(n-1)*|incy|
where:

n = number of vector elements specified in n

incy = increment argument for the array y specified in incy

Specify the data type as follows:

Routine Data Type for y

BLAS1$VSSWAP F-floating real

BLAS1$VDSWAP D-floating or G-floating real

BLAS1$VCSWAP F-floating complex

BLAS1$VZSWAP D-floating or G-floating complex

Previous Next Contents Index

privacy and legal statement

6117PRO_018.HTML

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	modify
mechanism:	by reference

OpenVMS usage:	floating_point
type:	F_floating, D_floating, or G_floating real
access:	write only
mechanism:	by reference

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

n	=	number of vector elements specified in n
incx	=	increment argument for the array x specified in incx

x	=	array specified in x
i	=	element of the vector x
incx	=	increment argument for the array x specified in incx

Routine	Data Type for x
BLAS1$VSSWAP	F-floating real
BLAS1$VDSWAP	D-floating or G-floating real
BLAS1$VCSWAP	F-floating complex
BLAS1$VZSWAP	D-floating or G-floating complex

n	=	number of vector elements specified in n
incy	=	increment argument for the array y specified in incy