The model set for reals, in general, is defined as one of the following:
![]()
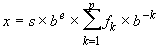
The following values apply to this model set:
| IEEE S_floating | 24 |
| Compaq [1] VAX F_floating [2] | 24 |
| IEEE T_floating | 53 |
| Compaq VAX D_floating [2] | 53 [3] |
| Compaq VAX G_floating [2] | 53 |
|
[1] Formerly DIGITAL
| |
| emin | emax | |
|---|---|---|
| IEEE S_floating | -125 | 128 |
| Compaq VAX F_floating [1] | -127 | 127 |
| IEEE T_floating | -1021 | 1024 |
| Compaq VAX D_floating [1] | -127 | 127 |
| Compaq VAX G_floating [1] | -1023 | 1023 |
|
[1] VMS only | ||
For x = 0, its exponent e and digits fk are defined to be zero.
The model set for single-precision real (REAL(4) or REAL*4) is defined as one of the following:
![]()
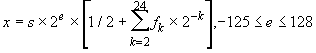
The following example demonstrates the general real model for x = 20.0 using a base (b) of 2:
x = 1 x 25 x (1 x 2-1 + 0 x 2-2 + 1 x 2-3)
x = 1 x 32 x (.5 + .125)
x = 32 x (.625)
x = 20.0