OpenVMS VAX RTL Mathematics (MTH$) Manual

Document revision date: 19 July 1999

OpenVMS VAX RTL Mathematics (MTH$) Manual

Contents

Index

Example


C C To compute the dot product of two vectors, x and y, C and return the result in DOTPR: C INTEGER INCX,INCY REAL X(20),Y(20),DOTPR INCX = 1 INCY = 1 N = 20 DOTPR = BLAS1$VSDOT(N,X,INCX,Y,INCY)

BLAS1$VxNRM2

The Obtain the Euclidean Norm of a Vector routine obtains the Euclidean norm of an n-element vector x , expressed as follows:
___________________________________ / x[1]**2 + x[2]**2 + ... + x[n]**2 \/

Format

BLAS1$VSNRM2 n ,x ,incx

BLAS1$VDNRM2 n ,x ,incx

BLAS1$VGNRM2 n ,x ,incx

BLAS1$VSCNRM2 n ,x ,incx

BLAS1$VDZNRM2 n ,x ,incx

BLAS1$VGWNRM2 n ,x ,incx
Use BLAS1$VSNRM2 for single-precision real operations.
Use BLAS1$VDNRM2 for double-precision real (D-floating) operations.
Use BLAS1$VGNRM2 for double-precision real (G-floating) operations. Use BLAS1$VSCNRM2 for single-precision complex operations.
Use BLAS1$VDZNRM2 for double-precision complex (D-floating) operations.
Use BLAS1$VGWNRM2 for double-precision complex (G-floating) operations.

RETURNS

OpenVMS usage: floating_point

type: F_floating, D_floating, or G_floating real

access: write only

mechanism: by value

The function value, called e_norm, is the Euclidean norm of the vector x . The data type of the function value is a real number; for the BLAS1$VSCNRM2, BLAS1$VDZNRM2, and BLAS1$VGWNRM2 routines, the data type of the function value is the real data type corresponding to the complex argument data type.

Arguments

n

OpenVMS usage: longword_signed

type: longword integer (signed)

access: read only

mechanism: by reference

Number of elements in vector x to be processed. The n argument is the address of a signed longword integer containing the number of elements.
x

OpenVMS usage: floating_point or complex_number

type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex

access: read only

mechanism: by reference, array reference

Array containing the elements to be accessed. All elements of array x are accessed only if the increment argument of x, called incx, is 1. The x argument is the address of a floating-point or floating-point complex number that is this array. This argument is an array of length at least:
1+(n-1)*|incx|
where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine Data Type for x

BLAS1$VSNRM2 F-floating real

BLAS1$VDNRM2 D-floating real

BLAS1$VGNRM2 G-floating real

BLAS1$VSCNRM2 F-floating complex

BLAS1$VDZNRM2 D-floating complex

BLAS1$VGWNRM2 G-floating complex

If n is less than or equal to 0, then e_norm is 0.0.
incx

OpenVMS usage: longword_signed

type: longword integer (signed)

access: read only

mechanism: by reference

Increment argument for the array x. The incx argument is the address of a signed longword integer containing the increment argument. If incx is greater than or equal to 0, then x is referenced forward in array x; that is, x[i] is referenced in:
x(1+(i-1)*incx)
where:

x = array specified in x

i = element of the vector x

incx = increment argument for the array x specified in incx

If you specify a negative value for incx, it is interpreted as the absolute value of incx.

Routine	Data Type for x
BLAS1$VSNRM2	F-floating real
BLAS1$VDNRM2	D-floating real
BLAS1$VGNRM2	G-floating real
BLAS1$VSCNRM2	F-floating complex
BLAS1$VDZNRM2	D-floating complex
BLAS1$VGWNRM2	G-floating complex

Description

BLAS1$VxNRM2 obtains the Euclidean norm of an n-element vector x , expressed as follows:
___________________________________ / x[1]**2 + x[2]**2 + ... + x[n]**2 \/
Vector x contains n elements that are accessed from array x by stepping incx elements at a time. The vector x is a real or complex single-precision or double-precision (D and G) n-element vector. The vector can be a row or a column of a matrix. Both forward and backward indexing are permitted.
The public-domain BLAS Level 1 xNRM2 routines require a positive value for incx. The Run-Time Library BLAS Level 1 routines interpret a negative value for incx as the absolute value of incx.
The algorithm does not provide a special case for incx = 0. Therefore, specifying 0 for incx has the effect of using vector operations to set e_norm as follows:
e_norm = n^0.5*|x[1]|
For BLAS1$VDNRM2, BLAS1$VGNRM2, BLAS1$VDZNRM2, and BLAS1$VGWNRM2 (the double-precision routines), the elements of the vector x are scaled to avoid intermediate overflow or underflow. BLAS1$VSNRM2 and BLAS1$VSCNRM2 (the single-precision routines) use a backup data type to avoid intermediate overflow or underflow.
Rounding in BLAS1$VxNRM2 occurs in a different order than in a sequential evaluation of the Euclidean norm. The final result may differ from the result of a sequential evaluation.

Example


C C To obtain the Euclidean norm of the vector x: C INTEGER INCX,N REAL X(20),E_NORM INCX = 1 N = 20 E_NORM = BLAS1$VSNRM2(N,X,INCX)

BLAS1$VxROT

The Apply a Givens Plane Rotation routine applies a Givens plane rotation to a pair of n-element vectors x and y .

Format

BLAS1$VSROT n ,x ,incx ,y ,incy ,c ,s

BLAS1$VDROT n ,x ,incx ,y ,incy ,c ,s

BLAS1$VGROT n ,x ,incx ,y ,incy ,c ,s

BLAS1$VCSROT n ,x ,incx ,y ,incy ,c ,s

BLAS1$VZDROT n ,x ,incx ,y ,incy ,c ,s

BLAS1$VWGROT n ,x ,incx ,y ,incy ,c ,s
Use BLAS1$VSROT for single-precision real operations.
Use BLAS1$VDROT for double-precision real (D-floating) operations.
Use BLAS1$VGROT for double-precision real (G-floating) operations. Use BLAS1$VCSROT for single-precision complex operations.
Use BLAS1$VZDROT for double-precision complex (D-floating) operations.
Use BLAS1$VWGROT for double-precision complex (G-floating) operations.
BLAS1$VCSROT, BLAS1$VZDROT, and BLAS1$VWGROT are real rotations applied to a complex vector.

RETURNS

None.

Arguments

n

OpenVMS usage: longword_signed

type: longword integer (signed)

access: read only

mechanism: by reference

Number of elements in vectors x and y to be rotated. The n argument is the address of a signed longword integer containing the number of elements to be rotated. If n is less than or equal to 0, then x and y are unchanged.
x

OpenVMS usage: floating_point or complex_number

type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex

access: modify

mechanism: by reference, array reference

Array containing the elements to be accessed. All elements of array x are accessed only if the increment argument of x, called incx, is 1. The x argument is the address of a floating-point or floating-point complex number that is this array. On entry, this argument is an array of length at least:
1+(n-1)*|incx|
where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine Data Type for x

BLAS1$VSROT F-floating real

BLAS1$VDROT D-floating real

BLAS1$VGROT G-floating real

BLAS1$VCSROT F-floating complex

BLAS1$VZDROT D-floating complex

BLAS1$VWGROT G-floating complex

If n is less than or equal to 0, then x and y are unchanged. If c equals 1.0 and s equals 0, then x and y are unchanged. If any element of x shares a memory location with an element of y , then the results are unpredictable.
On exit, x contains the rotated vector x , as follows:
x[i] <- c * x[i] + s * y[i]
where:

x = array x specified in x

y = array y specified in y

i = i = 1,2,...,n

c = rotation element generated by the BLAS1$VxROTG routines

s = rotation element generated by the BLAS1$VxROTG routines

incx

OpenVMS usage: longword_signed

type: longword integer (signed)

access: read only

mechanism: by reference

Increment argument for the array x. The incx argument is the address of a signed longword integer containing the increment argument. If incx is greater than or equal to 0, then x is referenced forward in array x; that is, x[i] is referenced in:
x(1+(i-1)*incx)
where:

x = array specified in x

i = element of the vector x

incx = increment argument for the array x specified in incx

If incx is less than 0, then x is referenced backward in array x; that is, x[i] is referenced in:
x(1+(n-i)*|incx|)
where:

x = array specified in x

n = number of vector elements specified in n

i = element of the vector x

incx = increment argument for the array x specified in incx

y

OpenVMS usage: floating_point or complex_number

type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex

access: modify

mechanism: by reference, array reference

Array containing the elements to be accessed. All elements of array y are accessed only if the increment argument of y, called incy, is 1. The y argument is the address of a floating-point or floating-point complex number that is this array. On entry, this argument is an array of length at least:
1+(n-1)*|incx|
where:

n = number of vector elements specified in n

incx = increment argument for the array x specified in incx

Specify the data type as follows:

Routine Data Type for y

BLAS1$VSROT F-floating real

BLAS1$VDROT D-floating real

BLAS1$VGROT G-floating real

BLAS1$VCSROT F-floating complex

BLAS1$VZDROT D-floating complex

BLAS1$VWGROT G-floating complex

If n is less than or equal to 0, then x and y are unchanged. If c equals 1.0 and s equals 0, then x and y are unchanged. If any element of x shares a memory location with an element of y , then the results are unpredictable.
On exit, y contains the rotated vector y , as follows:
y[i] <- -s * x[i] + c * y[i]
where:

x = array x specified in x

y = array y specified in y

i = i = 1,2,...,n

c = real rotation element (can be generated by the BLAS1$VxROTG routines)

s = complex rotation element (can be generated by the BLAS1$VxROTG routines)

incy

OpenVMS usage: longword_signed

type: longword integer (signed)

access: read only

mechanism: by reference

Increment argument for the array y. The incy argument is the address of a signed longword integer containing the increment argument. If incy is greater than or equal to 0, then y is referenced forward in array y; that is, y[i] is referenced in:
y(1+(i-1)*incy)
where:

y = array specified in y

i = element of the vector y

incy = increment argument for the array y specified in incy

If incy is less than 0, then y is referenced backward in array y; that is, y[i] is referenced in:
y(1+(n-i)*|incy|)
where:

y = array specified in y

n = number of vector elements specified in n

i = element of the vector y

incy = increment argument for the array y specified in incy

c

OpenVMS usage: floating_point

type: F_floating, D_floating, or G_floating real

access: read only

mechanism: by reference

First rotation element, which can be interpreted as the cosine of the angle of rotation. The c argument is the address of a floating-point or floating-point complex number that is this vector element. The c argument is the first rotation element generated by the BLAS1$VxROTG routines.
Specify the data type (which is always real) as follows:

Routine Data Type for c

BLAS1$VSROT and BLAS1$VCSROT F-floating real

BLAS1$VDROT and BLAS1$VZDROT D-floating real

BLAS1$VGROT and BLAS1$VWGROT G-floating real

s

OpenVMS usage: floating_point or complex_number

type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex

access: read only

mechanism: by reference

Second rotation element, which can be interpreted as the sine of the angle of rotation. The s argument is the address of a floating-point or floating-point complex number that is this vector element. The s argument is the second rotation element generated by the BLAS1$VxROTG routines.
Specify the data type (which can be either real or complex) as follows:

Routine Data Type for s

BLAS1$VSROT and BLAS1$VCSROT F-floating real or F-floating complex

BLAS1$VDROT and BLAS1$VZDROT D-floating real or D-floating complex

BLAS1$VGROT and BLAS1$VWGROT G-floating real or G-floating complex

Routine	Data Type for x
BLAS1$VSROT	F-floating real
BLAS1$VDROT	D-floating real
BLAS1$VGROT	G-floating real
BLAS1$VCSROT	F-floating complex
BLAS1$VZDROT	D-floating complex
BLAS1$VWGROT	G-floating complex

Routine	Data Type for y
BLAS1$VSROT	F-floating real
BLAS1$VDROT	D-floating real
BLAS1$VGROT	G-floating real
BLAS1$VCSROT	F-floating complex
BLAS1$VZDROT	D-floating complex
BLAS1$VWGROT	G-floating complex

Routine	Data Type for c
BLAS1$VSROT and BLAS1$VCSROT	F-floating real
BLAS1$VDROT and BLAS1$VZDROT	D-floating real
BLAS1$VGROT and BLAS1$VWGROT	G-floating real

Routine	Data Type for s
BLAS1$VSROT and BLAS1$VCSROT	F-floating real or F-floating complex
BLAS1$VDROT and BLAS1$VZDROT	D-floating real or D-floating complex
BLAS1$VGROT and BLAS1$VWGROT	G-floating real or G-floating complex

Description

BLAS1$VSROT, BLAS1$VDROT, and BLAS1$VGROT apply a real Givens plane rotation to a pair of real vectors. BLAS1$VCSROT, BLAS1$VZDROT, and BLAS1$VWGROT apply a real Givens plane rotation to a pair of complex vectors. The vectors x and y are real or complex single-precision or double-precision (D and G) vectors. The vectors can be rows or columns of a matrix. Both forward and backward indexing are permitted. The routine name determines the data type you should specify for arguments x and y. Specify the same data type for each of these arguments.
The Givens plane rotation is applied to n elements, where the elements to be rotated are contained in vectors x and y (i equals 1,2,...,n). These elements are accessed from arrays x and y by stepping incx and incy elements at a time. The cosine and sine of the angle of rotation are c and s, respectively. The arguments c and s are usually generated by the BLAS Level 1 routine BLAS1$VxROTG, using a=x and b=y :

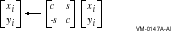
The BLAS1$VxROT routines can be used to introduce zeros selectively into a matrix.

Example


C C To rotate the first two rows of a matrix and zero C out the element in the first column of the second row: C INTEGER INCX,N REAL X(20,20),A,B,C,S INCX = 20 N = 20 A = X(1,1) B = X(2,1) CALL BLAS1$VSROTG(A,B,C,S) CALL BLAS1$VSROT(N,X,INCX,X(2,1),INCX,C,S)

C 
C To rotate the first two rows of a matrix and zero 
C out the element in the first column of the second row: 
C 
        INTEGER INCX,N 
        REAL X(20,20),A,B,C,S 
        INCX = 20 
        N = 20 
        A = X(1,1) 
        B = X(2,1) 
        CALL BLAS1$VSROTG(A,B,C,S) 
        CALL BLAS1$VSROT(N,X,INCX,X(2,1),INCX,C,S)

Contents

Index

privacy and legal statement

6117PRO_017.HTML

OpenVMS usage:	floating_point
type:	F_floating, D_floating, or G_floating real
access:	write only
mechanism:	by value

OpenVMS usage:	longword_signed
type:	longword integer (signed)
access:	read only
mechanism:	by reference

OpenVMS usage:	floating_point or complex_number
type:	F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access:	read only
mechanism:	by reference, array reference

n	=	number of vector elements specified in n
incx	=	increment argument for the array x specified in incx

x	=	array specified in x
i	=	element of the vector x
incx	=	increment argument for the array x specified in incx

x	=	array x specified in x
y	=	array y specified in y
i	=	i = 1,2,...,n
c	=	rotation element generated by the BLAS1$VxROTG routines
s	=	rotation element generated by the BLAS1$VxROTG routines

y	=	array specified in y
i	=	element of the vector y
incy	=	increment argument for the array y specified in incy