Document revision date: 19 July 1999
[Compaq] [Go to the documentation home page] [How to order documentation] [Help on this site] [How to contact us]
[OpenVMS documentation]

OpenVMS VAX RTL Mathematics (MTH$) Manual
Previous Contents Index

Part 3
Vector MTH$ Reference Section

 The Vector MTH$ Reference Section provides detailed descriptions of two sets of vector routines provided by the OpenVMS RTL Mathematics (MTH$) Facility, BLAS Level 1 and FOLR. The BLAS Level 1 are the Basic Linear Algebraic Subroutines designed by Lawson, Hanson, Kincaid, and Krogh (1978). The FOLR (First Order Linear Recurrence) routines provide a vectorized algorithm for the linear recurrence relation.

BLAS1$VIxAMAX

The Obtain the Index of the First Element of a Vector Having the Largest Absolute Value routine finds the index of the first occurrence of a vector element having the maximum absolute value.

Format

BLAS1$VISAMAX n ,x ,incx

BLAS1$VIDAMAX n ,x ,incx

BLAS1$VIGAMAX n ,x ,incx

BLAS1$VICAMAX n ,x ,incx

BLAS1$VIZAMAX n ,x ,incx

BLAS1$VIWAMAX n ,x ,incx

Use BLAS1$VISAMAX for single-precision real operations.
Use BLAS1$VIDAMAX for double-precision real (D-floating) operations.
Use BLAS1$VIGAMAX for double-precision real (G-floating) operations. Use BLAS1$VICAMAX for single-precision complex operations.
Use BLAS1$VIZAMAX for double-precision complex (D-floating) operations.
Use BLAS1$VIWAMAX for double-precision complex (G-floating) operations.

RETURNS


OpenVMS usage: longword_signed
type: longword integer (signed)
access: write only
mechanism: by value

For the real versions of this routine, the function value is the index of the first occurrence of a vector element having the maximum absolute value, as follows: 


  |x[i]| = max {|x[j]| for j=1,2,...,n}

For the complex versions of this routine, the function value is the index of the first occurrence of a vector element having the largest sum of the absolute values of the real and imaginary parts of the vector elements, as follows: 


  |Re(x[i])| + |Im(x[i])|= max {|Re(x[j])| + |Im(x[j])| for j=1,2,...,n}

Arguments

n


OpenVMS usage: longword_signed
type: longword integer (signed)
access: read only
mechanism: by reference

Number of elements in vector x . The n argument is the address of a signed longword integer containing the number of elements. If you specify a negative value or 0 for n, 0 is returned.

x


OpenVMS usage: floating_point or complex_number
type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access: read only
mechanism: by reference, array reference

Array containing the elements to be accessed. All elements of array x are accessed only if the increment argument of x, called incx, is 1. The x argument is the address of a floating-point or floating-point complex number that is this array. This argument is an array of length at least

1+(n-1)*|incx|

where:
n = number of vector elements specified in n
incx = increment argument for the array x specified in incx

Specify the data type as follows:
Routine Data Type for x
BLAS1$VISAMAX F-floating real
BLAS1$VIDAMAX D-floating real
BLAS1$VIGAMAX G-floating real
BLAS1$VICAMAX F-floating complex
BLAS1$VIZAMAX D-floating complex
BLAS1$VIWAMAX G-floating complex

If n is less than or equal to 0, then imax is 0.

incx


OpenVMS usage: longword_signed
type: longword integer (signed)
access: read only
mechanism: by reference

Increment argument for the array x. The incx argument is the address of a signed longword integer containing the increment argument. If incx is greater than or equal to 0, then x is referenced forward in array x; that is, x_i is referenced as:

x(1+(i-1)*incx)

where:
x = array specified in x
i = element of the vector x
incx = increment argument for the array x specified in incx

If you specify a negative value for incx, it is interpreted as the absolute value of incx.

Description

BLAS1$VISAMAX, BLAS1$VIDAMAX, and BLAS1$VIGAMAX find the index, i, of the first occurrence of a vector element having the maximum absolute value. BLAS1$VICAMAX, BLAS1$VIZAMAX, and BLAS1$VIWAMAX find the index, i, of the first occurrence of a vector element having the largest sum of the absolute values of the real and imaginary parts of the vector elements.

Vector x contains n elements that are accessed from array x by stepping incx elements at a time. The vector x is a real or complex single-precision or double-precision (D and G) n-element vector. The vector can be a row or a column of a matrix. Both forward and backward indexing are permitted.

BLAS1$VISAMAX, BLAS1$VIDAMAX, and BLAS1$VIGAMAX determine the smallest integer i of the n-element vector x such that: 


  |x[i]| = max {|x[j]| for j=1,2,...,n}

BLAS1$VICAMAX, BLAS1$VIZAMAX, and BLAS1$VIWAMAX determine the smallest integer i of the n-element vector x such that: 


  |Re(x[i])| + |Im(x[i])|= max {|Re(x[j])| + |Im(x[j])| for j=1,2,...,n}

You can use the BLAS1$VIxAMAX routines to obtain the pivots in Gaussian elimination.

The public-domain BLAS Level 1 IxAMAX routines require a positive value for incx. The Run-Time Library BLAS Level 1 routines interpret a negative value for incx as the absolute value of incx.

The algorithm does not provide a special case for incx = 0. Therefore, specifying 0 for incx has the effect of setting imax equal to 1 using vector operations.

Example


C 
C To obtain the index of the element with the maximum 
C absolute value. 
C 
        INTEGER IMAX,N,INCX 
        REAL X(40) 
        INCX = 2 
        N = 20 
        IMAX = BLAS1$VISAMAX(N,X,INCX)

BLAS1$VxASUM

The Obtain the Sum of the Absolute Values of the Elements of a Vector routine determines the sum of the absolute values of the elements of the n-element vector x .

Format

BLAS1$VSASUM n ,x ,incx

BLAS1$VDASUM n ,x ,incx

BLAS1$VGASUM n ,x ,incx

BLAS1$VSCASUM n ,x ,incx

BLAS1$VDZASUM n ,x ,incx

BLAS1$VGWASUM n ,x ,incx

Use BLAS1$VSASUM for single-precision real operations.
Use BLAS1$VDASUM for double-precision real (D-floating) operations.
Use BLAS1$VGASUM for double-precision real (G-floating) operations. Use BLAS1$VSCASUM for single-precision complex operations.
Use BLAS1$VDZASUM for double-precision complex (D-floating) operations.
Use BLAS1$VGWASUM for double-precision complex (G-floating) operations.

RETURNS


OpenVMS usage: floating_point
type: F_floating, D_floating, or G_floating real
access: write only
mechanism: by value

The function value, called sum, is the sum of the absolute values of the elements of the vector x . The data type of the function value is a real number; for the BLAS1$VSCASUM, BLAS1$VDZASUM, and BLAS1$VGWASUM routines, the data type of the function value is the real data type corresponding to the complex argument data type.

Arguments

n


OpenVMS usage: longword_signed
type: longword integer (signed)
access: read only
mechanism: by reference

Number of elements in vector x to be added. The n argument is the address of a signed longword integer containing the number of elements.

x


OpenVMS usage: floating_point or complex_number
type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access: read only
mechanism: by reference, array reference

Array containing the elements to be accessed. All elements of array x are accessed only if the increment argument of x, called incx, is 1. The x argument is the address of a floating-point or floating-point complex number that is this array. This argument is an array of length at least:

1+(n-1)*|incx|

where:
n = number of vector elements specified in n
incx = increment argument for the array x specified in incx

Specify the data type as follows:
Routine Data Type for x
BLAS1$VSASUM F-floating real
BLAS1$VDASUM D-floating real
BLAS1$VGASUM G-floating real
BLAS1$VSCASUM F-floating complex
BLAS1$VDZASUM D-floating complex
BLAS1$VGWASUM G-floating complex

If n is less than or equal to 0, then sum is 0.0.

incx


OpenVMS usage: longword_signed
type: longword integer (signed)
access: read only
mechanism: by reference

Increment argument for the array x. The incx argument is the address of a signed longword integer containing the increment argument. If incx is greater than or equal to 0, then x is referenced forward in array x; that is, x_i is referenced in:

x(1+(i-1)*incx)

where:
x = array specified in x
i = element of the vector x
incx = increment argument for the array x specified in incx

If you specify a negative value for incx, it is interpreted as the absolute value of incx.

Description

BLAS1$VSASUM, BLAS1$VDASUM, and BLAS1$VGASUM obtain the sum of the absolute values of the elements of the n-element vector x . BLAS1$VSCASUM, BLAS1$VDZASUM, and BLAS1$VGWASUM obtain the sum of the absolute values of the real and imaginary parts of the elements of the n-element vector x .

Vector x contains n elements that are accessed from array x by stepping incx elements at a time. The vector x is a real or complex single-precision or double-precision (D and G) n-element vector. The vector can be a row or a column of a matrix. Both forward and backward indexing are permitted.

BLAS1$VSASUM, BLAS1$VDASUM, and BLAS1$VGASUM compute the sum of the absolute values of the elements of x , which is expressed as follows:

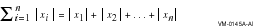
BLAS1$VSCASUM, BLAS1$VDZASUM, and BLAS1$VGWASUM compute the sum of the absolute values of the real and imaginary parts of the elements of x , which is expressed as follows:

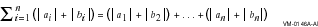
where |x[i]| = (a[i], b[i])

and |a[i]| + |b[i]| = |real| + |imaginary|

The public-domain BLAS Level 1 xASUM routines require a positive value for incx. The Run-Time Library BLAS Level 1 routines interpret a negative value for incx as the absolute value of incx.

The algorithm does not provide a special case for incx = 0. Therefore, specifying 0 for incx has the effect of computing n*|x[1]| using vector operations.

Rounding in the summation occurs in a different order than in a sequential evaluation of the sum, so the final result may differ from the result of a sequential evaluation.

Example


C 
C To obtain the sum of the absolute values of the 
C elements of vector x: 
C 
        INTEGER N,INCX 
        REAL X(20),SUM 
        INCX = 1 
        N = 20 
        SUM = BLAS1$VSASUM(N,X,INCX)

BLAS1$VxAXPY

The Multiply a Vector by a Scalar and Add a Vector routine computes ax + y , where a is a scalar number and x and y are n-element vectors.

Format

BLAS1$VSAXPY n ,a ,x ,incx ,y ,incy

BLAS1$VDAXPY n ,a ,x ,incx ,y ,incy

BLAS1$VGAXPY n ,a ,x ,incx ,y ,incy

BLAS1$VCAXPY n ,a ,x ,incx ,y ,incy

BLAS1$VZAXPY n ,a ,x ,incx ,y ,incy

BLAS1$VWAXPY n ,a ,x ,incx ,y ,incy

Use BLAS1$VSAXPY for single-precision real operations.
Use BLAS1$VDAXPY for double-precision real (D-floating) operations.
Use BLAS1$VGAXPY for double-precision real (G-floating) operations. Use BLAS1$VCAXPY for single-precision complex operations.
Use BLAS1$VZAXPY for double-precision complex (D-floating) operations.
Use BLAS1$VWAXPY for double-precision complex (G-floating) operations.

RETURNS

None.

Arguments

n


OpenVMS usage: longword_signed
type: longword integer (signed)
access: read only
mechanism: by reference

Number of elements in vectors x and y . The n argument is the address of a signed longword integer containing the number of elements. If n is less than or equal to 0, then y is unchanged.

a


OpenVMS usage: floating_point or complex_number
type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access: read only
mechanism: by reference, array reference

Scalar multiplier for the array x. The a argument is the address of a floating-point or floating-point complex number that is this multiplier. If a equals 0, then y is unchanged. If a shares a memory location with any element of the vector y , results are unpredictable. Specify the same data type for arguments a, x, and y.

x


OpenVMS usage: floating_point or complex_number
type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access: read only
mechanism: by reference, array reference

Array containing the elements to be accessed. All elements of array x are accessed only if the increment argument of x, called incx, is 1. The x argument is the address of a floating-point or floating-point complex number that is this array. The length of this array is at least:

1+(n-1)*|incx|

where:
n = number of vector elements specified in n
incx = increment argument for the array x specified in incx

Specify the data type as follows:
Routine Data Type for x
BLAS1$VSAXPY F-floating real
BLAS1$VDAXPY D-floating real
BLAS1$VGAXPY G-floating real
BLAS1$VCAXPY F-floating complex
BLAS1$VZAXPY D-floating complex
BLAS1$VWAXPY G-floating complex

If any element of x shares a memory location with an element of y , the results are unpredictable.

incx


OpenVMS usage: longword_signed
type: longword integer (signed)
access: read only
mechanism: by reference

Increment argument for the array x. The incx argument is the address of a signed longword integer containing the increment argument. If incx is greater than or equal to 0, then x is referenced forward in array x; that is, x[i] is referenced in:

x(1+(i-1)*incx)

where:
x = array specified in x
i = element of the vector x
incx = increment argument for the array x specified in incx

If incx is less than 0, then x is referenced backward in array x; ) that is, x[i] is referenced in:

x(1+(n-i)*|incx|)

where:
x = array specified in x
n = number of vector elements specified in n
i = element of the vector x
incx = increment argument for the array x specified in incx

y


OpenVMS usage: floating_point or complex_number
type: F_floating, D_floating, G_floating real or F_floating, D_floating, G_floating complex
access: modify
mechanism: by reference, array reference

On entry, array containing the elements to be accessed. All elements of array y are accessed only if the increment argument of y, called incy, is 1. The y argument is the address of a floating-point or floating-point complex number that is this array. The length of this array is at least:

1+(n-1)*|incy|

where:
n = number of vector elements specified in n
incy = increment argument for the array y specified in incy

Specify the data type as follows:
Routine Data Type for y
BLAS1$VSAXPY F-floating real
BLAS1$VDAXPY D-floating real
BLAS1$VGAXPY G-floating real
BLAS1$VCAXPY F-floating complex
BLAS1$VZAXPY D-floating complex
BLAS1$VWAXPY G-floating complex

If n is less than or equal to 0, then y is unchanged. If any element of x shares a memory location with an element of y , the results are unpredictable.

On exit, y contains an array of length at least:

1+(n-1)*|incy|

where:
n = number of vector elements specified in n
incy = increment argument for the array y specified in incy

After the call to BLAS1$VxAXPY, y[i] is set equal to:

y[i]+a*x[i]

where:
y = the vector y
i = element of the vector x or y
a = scalar multiplier for the vector x specified in a
x = the vector x

incy


OpenVMS usage: longword_signed
type: longword integer (signed)
access: read only
mechanism: by reference

Increment argument for the array y. The incy argument is the address of a signed longword integer containing the increment argument. If incy is greater than or equal to 0, then y is referenced forward in array y; that is, (y[i]) is referenced in:

Previous Next Contents Index

  [Go to the documentation home page] [How to order documentation] [Help on this site] [How to contact us]  
  privacy and legal statement  
6117PRO_015.HTML