| Previous | Contents | Index |
Integer data lengths can be one, two, four, or eight bytes in length.
Integer data is signed with the sign bit being 0 (zero) for positive numbers and 1 for negative numbers.
To improve performance, avoid using 2-byte or 1-byte integer
declarations (see Chapter 5).
8.2.1 Integer Declarations and FORTRAN Command Qualifiers
The default size used for an INTEGER data declaration without a kind parameter (or size specifier) is INTEGER (KIND=4) (same as INTEGER*4), unless you do one of the following:
Intrinsic INTEGER (KIND=1) or INTEGER*1 signed values range from --128 to 127 and are stored in a two's complement representation. For example:
+22 = 16(hex) -7 = F9(hex) |
INTEGER (KIND=1) or INTEGER*1 values are stored in one byte, as shown in Figure 8-1.
Figure 8-1 INTEGER (KIND =1) or INTEGER*1 Representation

Intrinsic INTEGER (KIND=2) or INTEGER*2 signed values range from --32,768 to 32,767 and are stored in a two's complement representation. For example:
+22 = 0016(hex) -7 = FFF9(hex) |
INTEGER (KIND=2) or INTEGER*2 values are stored in two contiguous bytes, as shown in Figure 8-2.
Figure 8-2 INTEGER (KIND =2) or INTEGER*2 Representation
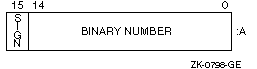
Intrinsic INTEGER (KIND=4) or INTEGER*4 signed values range from --2,147,483,648 to 2,147,483,647 and are stored in a two's complement representation. INTEGER (KIND=4) or INTEGER*4 values are stored in four contiguous bytes, as shown in Figure 8-3.
Figure 8-3 INTEGER (KIND =4) or INTEGER*4 Representation

Intrinsic INTEGER (KIND=8) or INTEGER*8 signed values range from --9,223,372,036,854,775,808 to 9,223,372,036,854,775,807 and are stored in a two's complement representation. INTEGER*8 or INTEGER (KIND=8) values are stored in eight contiguous bytes, as shown in Figure 8-4.
Figure 8-4 INTEGER (KIND =8) or INTEGER*8 Representation

For More Information:
Logical data can be one, two, four, or eight bytes in length.
The default size used for a LOGICAL data declaration without a kind parameter (or size specifier) is LOGICAL (KIND=4) (same as LOGICAL*4), unless you do one of the following:
To improve performance, avoid using 2-byte or 1-byte logical declarations (see Chapter 5).
Intrinsic LOGICAL*1 or LOGICAL (KIND=1) values are stored in a single byte.
Logical (intrinsic) values can also be stored in the following sizes of contiguous bytes starting on an arbitrary byte boundary:
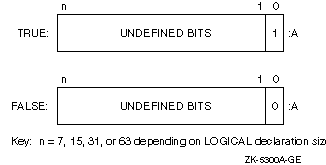
The low-order bit determines whether the logical value is true or false. Logical variables can also be interpreted as integer data (an extension to the Fortran 90 standard). For example, in addition to having logical values .TRUE. and .FALSE., LOGICAL*1 data can also have values in the range --128 to 127.
LOGICAL*1, LOGICAL*2, LOGICAL*4, and LOGICAL*8 data representations appear in Figure 8-5.
Figure 8-5 LOGICAL Representations
For More Information:
Floating-point numbers are stored on OpenVMS Alpha systems in one of the following IEEE or VAX little endian binary floating-point formats, as follows:
COMPLEX numbers use a pair of little endian REAL values to denote the real and imaginary parts of the data, as follows:
To specify the floating-point format used in memory, use the FORTRAN command /FLOAT qualifier. If you do not specify the /FLOAT (or /G_FLOAT) qualifier, the following formats are used:
To change the default size for REAL and COMPLEX declarations, use the FORTRAN command /REAL_SIZE qualifier.
To change the default size for DOUBLE PRECISION declarations, use the FORTRAN command /DOUBLE_SIZE qualifier.
All floating-point formats represent fractions using sign-magnitude notation, with the binary radix point to the right of the most-significant bit. Fractions are assumed to be normalized, and therefore the most-significant bit is not stored. This is called "hidden bit normalization".
With IEEE data, the hidden bit is assumed to be 1 unless the exponent is 0. If the exponent equals 0, then the value represented is denormalized (subnormal) or plus or minus 0 (zero).
With VAX data, the hidden bit is assumed to be 1.
For an explanation of the representation of NaN, Infinity, and related
IEEE exceptional values on Alpha systems, see Section 8.4.7.
8.4.1 REAL, COMPLEX, and DOUBLE PRECISION Declarations and FORTRAN Qualifiers
The default size for REAL, COMPLEX, and DOUBLE PRECISION data declarations are as follows:
You can explicitly declare the length of a REAL or a COMPLEX declaration using a kind parameter or specify DOUBLE PRECISION or DOUBLE COMPLEX.
Intrinsic REAL kinds are 4 (single precision) and 8 (double precision); intrinsic COMPLEX kinds are also 4 (single precision) and 8 (double precision). For example, REAL (KIND=4) requests single-precision floating-point data.
You can also use a size specifier, such as REAL*4, but be aware this is
an extension to the Fortran 90 standard.
8.4.2 REAL (KIND=4) or REAL*4 Representations
REAL (KIND=4) or REAL*4 data can be in IEEE S_float or VAX F_float
formats. This is the default data size for REAL declarations.
8.4.2.1 IEEE S_float Representation
Intrinsic REAL (KIND=4) or REAL*4 (single precision REAL) data occupies four contiguous bytes stored in IEEE S_float format. Bits are labeled from the right, 0 through 31, as shown in Figure 8-6.
Figure 8-6 IEEE S_float REAL (KIND =4) or REAL*4 Representation

The form of REAL (KIND=4) or REAL*4 data is sign magnitude, with:
The value of data is in the approximate range: 1.17549435E--38 (normalized) to 3.40282347E38. The IEEE denormalized limit is 1.40129846E--45.
The precision is approximately one part in 2**23, typically seven
decimal digits.
8.4.2.2 VAX F_float Representation
Intrinsic REAL (KIND=4) or REAL*4 F_float data occupies four contiguous bytes. Bits are labeled from the right, 0 through 31, as shown in Figure 8-7.
Figure 8-7 VAX F_float REAL (KIND =4) or REAL*4 Representation

The form of REAL (KIND=4) or REAL*4 F_float data is sign magnitude, where:
The value of data is in the approximate range: 0.293873588E--38 to 1.7014117E38.
The precision is approximately one part in 2**23, typically seven
decimal digits.
8.4.3 REAL (KIND=8) or REAL*8 Representations
REAL (KIND=8) or REAL*8 data can be in IEEE T_float, VAX G_float, or
VAX D_float formats.
8.4.3.1 IEEE T_float Representation
Intrinsic REAL (KIND=8) or REAL*8 (same as DOUBLE PRECISION) data occupies eight contiguous bytes stored in IEEE T_float format. Bits are labeled from the right, 0 through 63, as shown in Figure 8-8.
Figure 8-8 IEEE T_float REAL (KIND =8) or REAL*8 Representation

The form of REAL (KIND=8) or REAL*8 data is sign magnitude, with:
The value of data is in the approximate range: 2.2250738585072013D-308 (normalized) to 1.7976931348623158D308. The IEEE denormalized limit is 4.94065645841246544D-324.
The precision is approximately one part in 2**52, typically 15 decimal
digits.
8.4.3.2 VAX G_float Representation
Intrinsic REAL (KIND=8) or REAL*8 (same as DOUBLE PRECISION) G_float data occupies eight contiguous bytes. The bits are labeled from the right, 0 through 63, as shown in Figure 8-9.
Figure 8-9 VAX G_float REAL (KIND =8) or REAL*8 Representation

The form of REAL (KIND=8) or REAL*8 G_float data is sign magnitude, where:
The value of data is in the approximate range: 0.5562684646268004D--308 to 0.89884656743115785407D308.
The precision of G_float data is approximately one part in 2**52,
typically 15 decimal digits.
8.4.3.3 VAX D_float Representation
Intrinsic REAL (KIND=8) or REAL*8 (same as DOUBLE PRECISION) D_float data occupies eight contiguous bytes. Bits are labeled from the right, 0 through 63, as shown in Figure 8-10.
Figure 8-10 VAX D_float REAL (KIND =8) or REAL*8 Representation

The form of REAL (KIND=8) or REAL*8 D_float data is identical to an F_float real number, except for an additional 32 low-significance fraction bits. The exponent conventions and approximate range of values are the similar to those for F_float.
The value of data is in the approximate range: 0.2938735877055719D--38 to 1.70141183460469229D38.
The precision is approximately one part in 2**55, typically 16 decimal
digits. Calculations with D_float data on Alpha systems use G_float
precision (53-bit instead of 56-bit fraction).
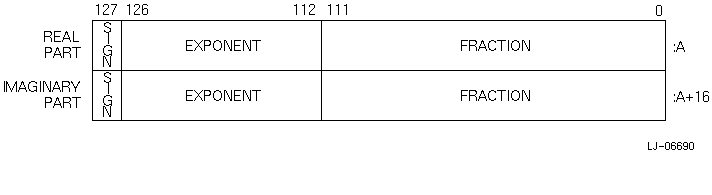
8.4.4 REAL (KIND=16) or REAL*16 X_float Representation
REAL*16 data occupies 16 contiguous bytes stored in X_float format. Bits are labeled from the right, 0 through 127, as shown in Figure 8-11.
Figure 8-11 X_float REAL (KIND =16) Floating-Point Data Representation

The form of REAL (KIND=16) data is sign magnitude, with:
The value of data is in the approximate range: 6.4751751194380251109244389582276465524996Q-4966 to 1.189731495357231765085759326628007016196477Q4932. The smallest normalized number is 3.362103143112093506262677817321753Q-4932. Unlike other floating-point formats, there is little if any performance penalty from using denormalized extended-precision numbers. This is because accessing denormalized REAL (KIND=16) numbers does not result in an arithmetic trap (the extended-precision format is emulated in software).
The precision is approximately one part in 2**112 or typically 33
decimal digits.
8.4.5 COMPLEX (KIND=4) or COMPLEX*8 Representations
COMPLEX (KIND=4) or COMPLEX*4 data can be in IEEE S_float or VAX F_float formats. This is the default data size for COMPLEX declarations.
Intrinsic COMPLEX (KIND=4) or COMPLEX*8 (single-precision COMPLEX) data is eight contiguous bytes containing a pair of REAL (KIND=4) or REAL*4 values stored in IEEE S_float format or VAX F_float format.
The low-order four bytes contain REAL (KIND=4) data that represents the real part of the complex number. The high-order four bytes contain REAL (KIND=4) data that represents the imaginary part of the complex number,
The limits (and underflow characteristics for S_float numbers) for REAL (KIND=4) or REAL*4 apply to the two separate real and imaginary parts of a COMPLEX (KIND=4) or COMPLEX*8 number. Like REAL (KIND=4) numbers, the sign bit representation is 0 (zero) for positive numbers and 1 for negative numbers.
Figure 8-12 shows the IEEE S_float representation of COMPLEX (KIND=4) or COMPLEX*8 numbers.
Figure 8-12 IEEE S_float COMPLEX (KIND =4) or COMPLEX*8 Representation
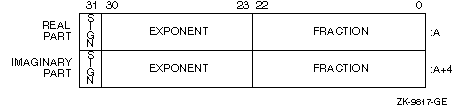
Figure 8-13 shows the VAX F_float representation of COMPLEX (KIND=4) or COMPLEX*8 numbers.
Figure 8-13 VAX F_float COMPLEX (KIND =4) or COMPLEX*8 Representation
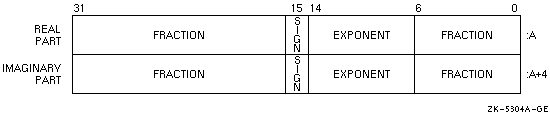
COMPLEX (KIND=8) or COMPLEX*16 data can be in IEEE T_float, VAX G_float, or VAX D_float formats.
Intrinsic COMPLEX (KIND=8) or COMPLEX*16 (same as DOUBLE COMPLEX) data is 16 contiguous bytes containing a pair of REAL*8 values stored in IEEE T_float format, VAX G_float, or VAX D_float formats.
The low-order eight bytes contain REAL (KIND=8) data that represents the real part of the complex data. The high-order eight bytes contain REAL (KIND=8) data that represents the imaginary part of the complex data.
Like REAL (KIND=8) or REAL*8 numbers, the sign bit representation is 0 (zero) for positive numbers and 1 for negative numbers. The limits (and underflow characteristics for T_float numbers) apply to the two separate real and imaginary parts of a COMPLEX (KIND=8) or COMPLEX*16 number.
Figure 8-14 shows the IEEE T_float COMPLEX (KIND=8) or COMPLEX*16 representation.
Figure 8-14 IEEE T_float COMPLEX (KIND =8) or COMPLEX*16 Representation
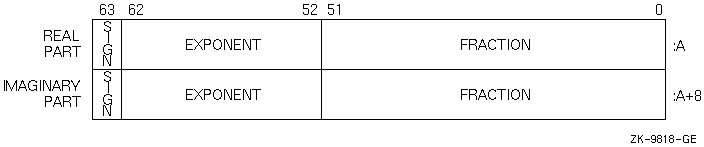
Figure 8-15 (G_float) and Figure 8-16 (D_float) show the representation of the VAX COMPLEX (KIND=8) or COMPLEX*16 numbers.
Figure 8-15 VAX G_float COMPLEX (KIND =8) or COMPLEX*16 Representation
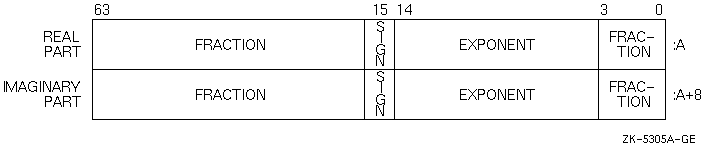
Figure 8-16 VAX D_float COMPLEX (KIND =8) or COMPLEX*16 Representation
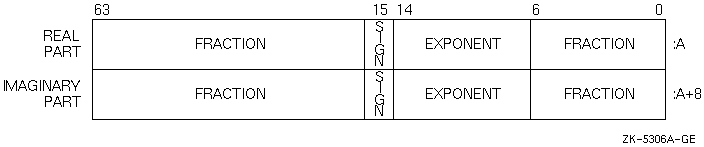
Beginning with Compaq Fortran Verision 7.3 for OpenVMS Alpha systems, the COMPLEX(KIND=16) or COMPLEX*32 intrinsic date type is now supported. It consists of a pair of REAL*16 values in Compaq IEEE style X_float format. For more information, see the online release notes and the following figure:
COMPLEX (KIND=16) or COMPLEX*32
Representation

For More Information:
Exceptional values usually result from a computation and include plus infinity, minus infinity, NaN, and denormalized numbers. Exceptional values and the representation of zero are associated only with IEEE S_float, T_float, and X_float formats (/FLOAT=IEEE_FLOAT qualifier), not with VAX floating-point formats. (VAX floating-point representation of minus (--) zero causes a reserved operand fault on VAX systems.)
Floating-point numbers can be one of the following:
A NaN or infinity value might result from a calculation that contains a divide by zero, overflow, or invalid data.
A denormalized number occurs when the result of a calculation falls within the denormalized range for that data type (subnormal value).
To control floating-point exception handling at run time for the main program, use the appropriate /IEEE_MODE qualifier keyword. For example, if an exceptional value is used in a calculation, an unrecoverable exception can occur unless you specify the appropriate /IEEE_MODE qualifier keyword. Denormalized numbers can be processed as is, set equal to zero with program continuation or a program stop, and generate warning messages (see Section 2.3.21).
Table 8-2 lists the hexadecimal (hex) values of the IEEE exceptional floating-point numbers in Alpha systems, for S_float (single precision), T_float (double precision), and X_float (extended precision) formats:
| Exceptional Number | Hex Value |
|---|---|
| S_float Representation | |
| Infinity (+) | Z ' 7F800000 ' |
| Infinity (-) | Z ' FF800000 ' |
| Zero (+0) | Z ' 00000000 ' |
| Zero (-0) | Z ' 80000000 ' |
| Quiet NaN (+) | From Z ' 7FC00000 ' to Z ' 7FFFFFFF ' |
| Signaling NaN (+) | From Z ' 7F800001 ' to Z ' 7FBFFFFF ' |
| T_float Representation | |
| Infinity (+) | Z ' 7FF0000000000000 ' |
| Infinity (-) | Z ' FFF0000000000000 ' |
| Zero (+0) | Z ' 0000000000000000 ' |
| Zero (-0) | Z ' 8000000000000000 ' |
| Quiet NaN (+) | From Z ' 7FF8000000000000 ' to Z ' 7FFFFFFFFFFFFFFF ' |
| Signaling NaN (+) | From Z ' 7FF0000000000001 ' to Z ' 7FF7FFFFFFFFFFFF ' |
| X_float Representation | |
| Infinity (+) | Z ' 7FFF0000000000000000000000000000 ' |
| Infinity (-) | Z ' FFFF0000000000000000000000000000 ' |
| Zero (+0) | Z ' 000000000000000000000000000000000 ' |
| Zero (-0) | Z ' 800000000000000000000000000000000 ' |
| Quiet NaN (+) | From Z ' 7FFF80000000000000000000000000000 ' to Z ' 7FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF ' |
| Signaling NaN (+) | From Z ' 7FFF00000000000000000000000000001 ' to Z ' 7FFF7FFFFFFFFFFFFFFFFFFFFFFFFFFFF ' |
Compaq Fortran supports IEEE exception handling, allowing you to test for infinity by using a comparison of floating-point data (such as generating positive infinity by using a calculation such as x=1.0/0 and comparing x to the calculated number).
The appropriate FORTRAN command /IEEE_MODE qualifier keyword allows program continuation when a calculation results in a divide by zero, overflow, or invalid data arithmetic exception, generating an exceptional value (a NaN or Infinity (+ or --)).
To test for a NaN when Compaq Fortran allows continuation for arithmetic exception, you can use the ISNAN intrinsic function. Example 8-1 shows how to use the ISNAN intrinsic function to test whether a REAL*8 (DOUBLE PRECISION) value contains a NaN.
| Example 8-1 Testing for a NaN Value |
|---|
DOUBLE PRECISION A, B, F
A = 0.
B = 0.
! Perform calculations with variables A and B
.
.
.
! f contains the value to check against a particular NaN
F = A / B
IF (ISNAN(F)) THEN
WRITE (6,*) '--> Variable F contains a NaN value <--'
ENDIF
! Inform user that f has the hardware quiet NaN value
! Perform calculations with variable F (or stop program early)
END
|
To allow continuation when a NaN (or other exceptional value) is encountered in a calculation, this program might be compiled with /FLOAT=IEEE_FLOAT and /IEEE_MODE=UNDERFLOW_TO_ZERO (or /IEEE_MODE=DENORM_RESULTS) qualifiers:
$ FORTRAN/FLOAT=IEEE_FLOAT/IEEE_MODE=UNDERFLOW_TO_ZERO ISNAN $ LINK ISNAN $ RUN ISNAN --> Variable F contains a NaN value <-- |
To enable additional run-time message reporting with traceback information (source line correlation), use the FORTRAN command qualifier /CHECK=FP_EXCEPTIONS.
The FP_CLASS intrinsic function is also available to check for exceptional values (see the Compaq Fortran Language Reference Manual).
For More Information:
| Previous | Next | Contents | Index |